MRUV
Considere três corpos A, B e C, que descrevem trajetórias retilíneas com velocidades variadas. As tabelas a seguir apresentam as velocidades nos instantes: 0 s, 1 s, 2 s, 3 s e 4 s.
B | C | ||||||
t (s) | v (m/s) | t (s) | v (m/s) | ||||
0 | 0 | 0 | 0 | 0 | |||
1 | 1 | 1 | 2 | 1 | 1 | ||
2 | 4 | 2 | 4 | 2 | 3 | ||
3 | 9 | 3 | 6 | 3 | 6 | ||
4 | 16 | 4 | 8 | 4 | 10 | ||
Observa-se que os três corpos descrevem movimentos variados, porém somente um, descreve movimento uniformemente variado. Qual deles descreve este movimento?
Definição
É chamado movimento uniformemente variado, aquele em que a aceleração escalar instantânea é constante e diferente de zero. Assim, pode-se concluir que a aceleração escalar do movimento uniformemente variado é igual à aceleração escalar média. Neste caso, a velocidade varia de maneira uniforme com o tempo.
No exemplo anterior, o corpo B descreve um movimento uniformemente variado, pois o aumento da velocidade é o mesmo para intervalos de tempos iguais.
Sabendo que a aceleração escalar do MUV é igual à aceleração escalar média, pode-se escrever:
Onde:
v ® velocidade no instante t
vo ® velocidade inicial
t ® tempo
a ® aceleração
Função horária do espaço
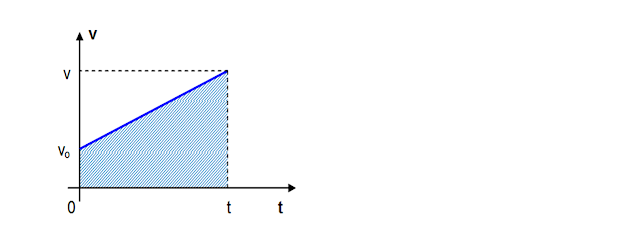
A função horária do espaço pode ser determinada usando a propriedade do gráfico v x t em que a área do gráfico é numericamente igual ao deslocamento. Sendo do 1º. Grau a função horária da velocidade (v = vo + a.t), o gráfico v x t será uma reta:
Onde:
So ® posição inicial
vo ® velocidade inicial
t ® tempo
a ® aceleração
É importante observar que é possível deduzir a função horária da velocidade a partir da função horária do espaço:
Exercícios resolvidos
1. Determine os valores do espaço inicial So, da velocidade inicial vo, da aceleração a e a função horária da velocidade referente às funções horárias do espaço a seguir dadas em unidades do SI:
2. A fórmula da posição de um móvel, no SI, é dada por S = 20 t - t 2. Em que instantes, em segundos, a posição desse móvel é s = 0?
a) 0 e 2
b) 0 e 4
c) 2 e 4
d) 3 e 6
e) 2 e 6
Resolução:
Para S = 0 , tem-se:
S = 20 t - t 2
0 = 20 t - t 2
t 2 = 20 t
t1 = 0
t2 = 20 s