TRABALHO TERMODINÂMICO
Para
que um corpo realize trabalho é condição necessária que ele aplique uma força e
desloque um corpo. Como uma amostra gasosa poderia realizar trabalho? O
objetivo deste estudo é responder a esta questão.
Trabalho
com pressão constante
Considere
uma dada massa de gás encerrada num cilindro dotado de um pistão móvel sem
atrito com as paredes do cilindro determinando uma pressão constante no gás.
Ao
fornecer uma quantidade de calor ao gás, este sofre um processo de expansão
isobárica passando de uma situação inicial com pressão po, volume Vo
e temperatura To, para uma situação final com pressão final po
(isobárica), volume V e temperatura T. O gás aplica uma força F no
êmbolo que sofre um deslocamento d,
da posição A até a posição B.
Pode-se observar que o gás está realizando
um trabalho, pois aplica uma força e esta força desloca o êmbolo. Pelos
conceitos estudados na mecânica, o trabalho é calculado pelo produto da força e
o deslocamento.
Sabendo
que a área do pistão é A, A força
aplicada pelo gás é F e o
deslocamento é x, tem-se:
Da
expressão do trabalho, verifica-se que ele pode ser positivo, negativo ou nulo.
Assim:
Volume
|
Trabalho feito pelo gás
|
Trabalho
|
Aumenta
|
Realizado
|
( + )
|
Diminui
|
Recebido
|
( – )
|
Constante
|
Não existente
|
Nulo
|
Trabalho com pressão variável
Caso numa transformação gasosa
de A para B ocorra uma variação de pressão do gás, pode-se calcular
numericamente o trabalho associado à transformação gasosa pela área
compreendida entre o gráfico e o eixo dos volumes no diagrama de Clapeyron.
Transformação Cíclica
Uma
transformação gasosa de um gás é dita cíclica (ou fechada), quando: o mesmo
parte de um estado inicial, passa por estados intermediários e retorna ao
estado inicial.
O trabalho total da transformação cíclica será calculado pela soma
algébrica dos trabalhos parciais:
Tciclo = TAB + TBC + TCA
Tciclo = A1 + 0 - A2
Verifica-se que a soma dos trabalhos é igual à diferença entre as áreas
A1 e A2, de forma que resta a área fechada (área do
ciclo).
Observe
que:
- Em toda transformação cíclica representada no diagrama pxV,
o trabalho realizado é fornecido pela área do ciclo.
-
sentido horário ® o
gás realiza trabalho (T > 0)
-
sentido anti-horário ® o
gás recebe trabalho (T < 0)
Exercícios
resolvidos
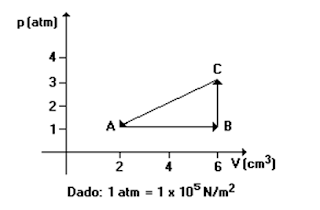
O trabalho realizado pelo gás na transformação AB é de:
a) 400J
b) 800J
c) 300J
d) 600J
e) 200J
Resolução:
Alternativa
A
2.
Um gás ideal sofre transformações segundo o ciclo dado no esquema p x V a
seguir.
O
trabalho total no ciclo ABCA é
a)
igual a - 0,4 J, sendo realizado sobre o gás.
b)
igual a - 0,8 J, significando que o gás está perdendo energia.
c)
realizado pelo gás, valendo + 0,4 J.
d)
realizado sobre o gás, sendo nulo.
e)
nulo, sendo realizado pelo gás.
Resolução:
O
trabalho no ciclo é numericamente igual à área interna do diagrama e como o
ciclo é anti-horário o trabalho é negativo:
Alternativa
A
Energia interna (U)
A energia interna de um gás é a soma de todas
as energias que se encontram na amostra gasosa. Para um gás ideal, essa energia
pode ser determinada pela energia cinética das moléculas (vibração e rotação)
e da energia potencial, devido a forças intermoleculares. Para um gás perfeito
monoatômico, a energia interna U é
dada por:
Como a energia interna de um gás é igual à
energia cinética das moléculas da amostra observa-se que a energia interna é
função exclusiva de sua temperatura absoluta. Assim é possível construir a
tabela a seguir:
Temperatura
|
Energia interna
|
|
Aumenta
|
Aumenta
|
DU > 0
|
Diminui
|
Diminui
|
DU < 0
|
Não se altera
|
Não se altera
|
DU = 0
|
PRIMEIRA
LEI DA TERMODINÂMICA
É
baseada no Princípio da Conservação da Energia e pode ser enunciada
assim:
“Todo
quantidade de calor Q absorvida (Q > 0) ou cedida (Q < 0) por um sistema,
é transformado em trabalho trocado com o meio, realizado por este sistema (T
> 0) ou sobre ele (T < 0), e energia interna, sofrendo um aumento (DU > 0) ou diminuição
(DU < 0) de forma
que:
Exercícios resolvidos
1. Um corpo recebe 180 Joules de calor de um outro corpo e
rejeita 40 Joules para o ambiente. Simultaneamente, o corpo realiza um trabalho
de 150 Joules. Qual foi a variação da energia interna do sistema termodinâmico?
Resolução:
O sistema termodinâmico recebeu uma quantidade de calor
efetiva de Q = 180 – 40 = 140 J e realizou um trabalho de 150 J. Assim, tem-se:
Q = T + DU
140 = 150 + DU
DU =
- 10 J
Resposta: A variação da energia interna do sistema
termodinâmico foi de –10 J.
2. A um sistema termodinâmico,
transfere-se 250 calorias em forma de calor. Verifica-se que o sistema se
expande, realizando um trabalho de 600 joules.
a) Considerando 1
cal = 4 J calcule a quantidade de energia transferida ao sistema, em joules.
b) Calcule a
variação de energia interna desse sistema.
Resolução:
a) O sistema recebeu uma quantidade de calor de 250 calorias.
Para transformar em joules deve-se multiplicar pelo equivalente mecânico dado
no texto (1
cal = 4 J).
Q
= 250 cal = 250 x 4 = 1000 J
b)
A variação da energia interna é dada por:
Q = T + DU
1.000 = 600 + DU
DU = 400
J
Resposta: O sistema recebeu 1000 J em forma de calor e a
variação de sua energia interna foi de 400 J.
Transformação
Isométrica
V = constante
|
||
DV
= 0
|
T = 0
|
DU = Q
|
Recebe
calor
|
U aumenta
|
T aumenta
|
Cede
calor
|
U diminuiu
|
T diminui
|
Transformação
Isotérmica
T = constante
|
|||
U = constante
|
DU = 0
|
Q = t
|
|
Recebe
calor
|
T
realizado
|
||
Cede
calor
|
T
recebido
|
||
Transformações
Adiabáticas
É a
transformação na qual não há troca de calor entre o gás e a sua vizinhança.
Normalmente
são transformações que ocorrem de modo muito rápido.
Q = 0 ® DU
= – T
|
|
Expansão
Adiabática
|
Compressão
Adiabática
|
O gás realiza trabalho às custas de sua energia interna
|
O gás recebe trabalho que se transforma em energia interna
|
U diminui
|
U aumenta
|
T diminui
|
T aumenta
|
Aplicações
Práticas
Por
que o conteúdo de um spray esfria quando pressionamos a válvula?
Ao
expandir-se, o gás realiza trabalho, sendo essa expansão rápida, podemos
considerar Q = 0.
Se,
Q = T + DU e Q = 0, tem-se: DU = – T
Como
o trabalho é positivo, significa que a energia interna diminuiu; consequentemente,
a temperatura também diminui, ou seja, o gás esfriou porque realizou trabalho
às custas da energia interna.
Por
que ao enchermos uma bola de futebol, a bomba se aquece?
Ocorre
compressão gasosa (T < 0), entretanto o
volume diminui e a energia interna aumenta, assim ocorre um aumento de
temperatura.
2ª. Lei da termodinâmica
Quando se pensa em motores e indústrias,
verifica-se que a 2ª. lei da termodinâmica possui uma maior aplicação, pois trata
do rendimento das máquinas térmicas.
Pode-se enunciar:

É
impossível a construção de uma máquina que,
operando
em um ciclo termodinâmico, converta
toda
a quantidade de calor recebido em trabalho.
Em outras palavras, pode-se afirmar que um dispositivo
termodinâmico nunca terá um rendimento de 100%.
Máquina
Térmica
Denomina-se máquina térmica o dispositivo que,
utilizando duas fontes térmicas, faz com que a energia térmica se converta em
energia mecânica (trabalho).
São
exemplos de máquinas térmicas o motor de automóvel, a locomotiva a vapor, as
turbinas a vapor usadas na geração de eletricidade.
Uma máquina térmica sempre estará recebendo calor
de uma fonte quente, mas uma parte deste calor é rejeitada para uma fonte fria
e o restante é transformado em trabalho.
Rendimento
de uma máquina térmica
O
rendimento de uma máquina térmica é a razão entre a energia útil (trabalho)
pela energia total (quantidade de calor da fonte quente) que a máquina recebe
para realizar trabalho.
Considerando:
h = rendimento;
T =
trabalho convertido através da energia térmica fornecida;
Q1 =quantidade de calor fornecida pela fonte de
aquecimento;
Q2
=quantidade de calor não transformada em trabalho, cedida para a
fonte fria.
São exemplos de rendimento de algumas máquinas térmicas:
- Locomotivas a vapor (rendimento cerca de 10%).
- Motores à gasolina
(rendimento nunca ultrapassa 30 %).
- Motores a diesel, que estão entre as máquinas térmicas mais
eficientes (rendimento em torno de 40%).
Ciclo de Carnot
Até meados do século XIX, achavam
possível construir uma máquina térmica ideal, que transformaria toda a energia
fornecida em trabalho, obtendo um rendimento total (100%).
Para
demonstrar que não seria possível, o engenheiro militar francês Nicolas Sadi
Carnot, propôs uma máquina teórica, ideal,
onde o rendimento seria o máximo possível. Este ciclo de rendimento
máximo passou a ser chamado ciclo de Carnot.
- A®B : expansão isotérmica. O sistema
recebe uma quantidade de calor da fonte de aquecimento.
- B®C : expansão adiabática. O sistema não
troca calor com as fontes térmicas.
- C®D : compressão isotérmica. O sistema
cede calor para a fonte de resfriamento.
- D®A : compressão adiabática. O sistema
não troca calor com as fontes térmicas.
Carnot
afirmava que o rendimento de uma máquina térmica dependia exclusivamente das
temperaturas das fontes fria e quente.
Como numa
máquina de Carnot, a quantidade de calor da fonte quente e da fonte fria são
proporcionais às suas temperaturas absolutas, tem:
Exercício resolvido
1. Uma máquina térmica, operando em um ciclo
de Carnot, trabalha entre as temperaturas de – 73ºC e 227ºC. Em cada ciclo, a
máquina recebe 500 J de calor da fonte quente. Analise as seguintes
afirmativas:
I. O
rendimento dessa máquina é de 40%.
II. O
trabalho realizado pela máquina é de 300 J.
III.
O calor rejeitado, por ciclo, para a fonte fria é de 200 J.
Está
correta ou estão corretas:
a) I
e II.
b) II e III.
c) I
e III.
d)
somente II.
e)
somente III.
Resolução:
Alternativa
B