LEIS DE KIRCHHOFF
Polaridade
e DDP dos elementos elétricos
Nos geradores ou
receptores, os pólos não dependem do sentido da corrente elétrica. O traço
menor é negativo e o traço maior é positivo.
O potencial do pólo B
é maior que do pólo A, assim:
VA – VB = - E
No caso
Para facilitar, vale
a regra:
“A ddp de um elemento
pode ser positivo ou negativo, valendo o sinal de entrada no elemento no
sentido adotado.”
Nos resistores, a
polaridade é determinada pelo sentido da corrente elétrica. O pólo positivo é o
de entrada da corrente elétrica e o negativo é o de saída da corrente elétrica.
VB – VA = - R . i
Cálculo
da ddp num ramo
Para se determinar a
ddp em um ramo, devem-se seguir os passos:
1º. Indicar as
polaridades de cada elemento;
2º. Verificar o
sentido de percurso a ser seguido;
3º. Somar
algebricamente as ddp dos elementos do ramo.
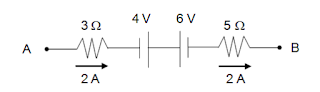
Considere o circuito
elétrico abaixo:
Qual
a ddp entre os pontos A e B?
Para
determinar a ddp, seguindo os passos informados anteriormente, tem-se:
UAB = + 3 . 2 – 4 + 6 + 5 . 2
UAB = 18 V
Chama-se nó de um
circuito elétrico, o ponto de encontro de três ou mais condutores.
A
soma das intensidades das correntes elétricas que
chegam
em
um nó é igual à soma das intensidades das
correntes
elétricas que saem deste nó.
2ª.
Lei de Kirchhoff – Lei das Malhas
Denomina-se
malha todo conjunto fechado de ramos, ou seja, é a parte do circuito que
corresponde a uma linha poligonal fechada.
A soma algébrica da d.d.p em uma malha (percurso fechado)
é nula.
Aplicação
Considere o
circuito da figura a seguir.
a) Utilize as leis
de Kirchhoff para encontrar as correntes i1, i2 e i3.
b) Encontre a
diferença de potencial VA – VB .
Resolução
a) Como os nós já
estão sinalizados pelas letras A e B e as correntes elétricas com sentidos
determinados, devem-se atribuir as polaridades dos elementos do circuito.
A seguir aplica-se
a primeira lei de Kirchhoff no nó A ou B.
Atribui-se a cada
malha independente um sentido arbitrário (horário ou anti-horário) de
percurso e na sequencia, aplicar a segunda lei de Kirchhoff:
Malha
a (partindo de B)
Malha b (partindo de B)
i3 = 2 i2
+ i2
Substituindo a
equação IV na equação III, tem-se:
22 i2 =
11
i2 = 0,5 A
i3 = 3 i2
i3 = 1,5 A
Substituindo na
equação II, tem-se:
i1 = 1,0 A
b) VA
– VB = +6 + 4 . 0,5
VA – VB
= 6 + 2
VA – VB = 8 V
Não se deve
esquecer que é necessário interpretar os resultados, lembrando que:
- quando a
intensidade da corrente elétrica resultar num sinal negativo deve-se inverter o
sentido da corrente;
- inverter as
polaridades das tensões que resultarem negativas.
- expressar as
respostas por números positivos.