Gravitação
Universal
Desde tempos muito remotos, o
homem observa o céu, tentando compreender este universo fantástico e seus
astros. Foram os filósofos gregos os primeiros que tentaram explicar o
movimento dos corpos celestes sem recorrer a mitos religiosos.
Sistema Geocêntrico
Cláudio
Ptolomeu (100-170), na sua famosa obra o Almagesto, propõe um sistema,
onde estabelecia que a Terra estava no centro do universo. A Lua e o Sol
descreviam órbitas circulares em torno da Terra. Quanto aos demais planetas,
descreviam órbitas circulares em torno de um centro, que por sua vez, descrevia
outra órbita circular ao redor da Terra. Esse artifício era necessário para
explicar as observações dos movimentos dos planetas no céu.
A
figura representa um diagrama simplificado do sistema geocêntrico de Ptolomeu.
Sistema Heliocêntrico
O
astrônomo Nicolau Copérnico (1473-1543), na sua obra Sobre a revolução dos
corpos celestes, propôs ser o Sol o centro do universo e os planetas
descrevem órbitas circulares em torno do Sol.
A
figura representa um diagrama simplificado do sistema heliocêntrico de
Copérnico.
Johannes
Kepler (1571-1630) herdou os registros das preciosas observações de seu mestre
Tycho Brahe (1546-1601), que lhe permitiram enunciar as leis que regem os
movimentos dos planetas.
Leis de Kepler
1.ª Lei – Lei das Órbitas
"As
órbitas dos planetas são elipses, nas quais o Sol ocupa um dos focos."
Os pontos A e B na figura representam
as posições quando o planeta está mais próximo do Sol, denominado de periélio e
quando está mais afastado do Sol, denominado de afélio.
2.ª Lei
– Lei das Áreas
"O
segmento de reta imaginário que une o centro do Sol ao centro do planeta
descreve áreas proporcionais aos intervalos de tempo gastos para
descrevê-las."
O movimento de cada planeta ao
longo da elipse não é uniforme. Quando se aproxima do periélio, seu movimento é
acelerado, sendo sua velocidade máxima neste ponto; quando se aproxima do afélio,
apresenta movimento retardado e sua velocidade é mínima no afélio. Para a
Terra, o máximo e o mínimo da velocidade são 30,2 km/s na posição próxima do
Sol e 29,3 km/s na mais afastada do Sol.
3.ª Lei
– Lei dos Períodos (Lei da Harmonia)
"Os
quadrados dos períodos de revolução dos planetas em torno do Sol são
diretamente proporcionais aos cubos dos raios médios de suas respectivas
órbitas".
Sejam dois planetas 1 e 2 descrevendo órbitas elípticas em torno do Sol, podemos escrever:
Observação
As
leis de Kepler são válidas para quaisquer corpos que gravitem em torno de outro
corpo de massa bem maior. Aplicam-se aos satélites naturais e artificiais.
Lei da Gravitação Universal
Conforme as leis de Kepler, os
movimentos dos planetas em torno do Sol não são uniformes. Portanto existe uma
aceleração, o que implica a presença de uma força resultante diferente de zero.
Newton concluiu que os planetas e o Sol interagem à distância, com forças
chamadas gravitacionais. Com sua alta capacidade de generalização e profundo
conhecimento da matemática, Newton percebeu que as forças gravitacionais são
funções do inverso do quadrado da distância entre o planeta e o Sol, e depende
diretamente das massas do planeta e do Sol.
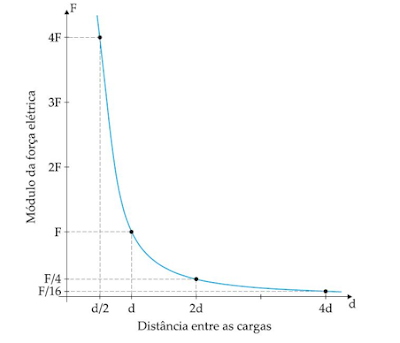
"Dois
corpos quaisquer exercem entre si uma força de atração gravitacional cuja
intensidade é diretamente proporcional ao produto de suas massas e inversamente
proporcional ao quadrado da distância que os separam."
Em que:
M1 e M2 são as massas dos corpos
d é a distância entre os corpos
G é uma constante válida para quaisquer dois corpos em
qualquer local do universo, denominada de constante de gravitação universal, o
valor de G é 6,67 x 10-11 Nm2/kg2.