Lei de Coulomb
Considere
duas partículas, A e B, eletrizados com cargas QA e QB,
respectivamente, e separados por uma distância d.
O físico Charles Coulomb observou que a força eletrostática trocada por estas partículas era diretamente proporcional às suas cargas,
e
inversamente proporcional ao quadrado da distância entre as cargas.
Assim, enuncia-se a Lei de
Coulomb:
"O módulo da força de atração ou repulsão entre cargas pontuais
é diretamente
proporcional ao produto das cargas e inversamente
proporcional ao
quadrado da distância entre elas.”
Direção: é a
reta que une os centros geométricos dos corpos eletrizados.
Sentido: é
dado pela Lei de Du Fay.
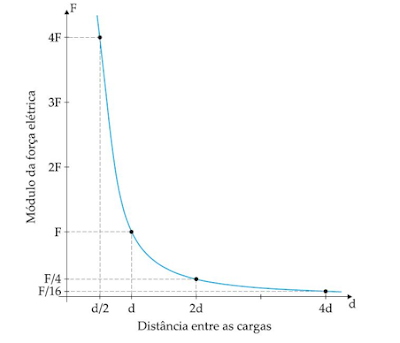
Gráfico F = f(d)
Pela Lei de Coulomb observa-se que a força e a distância
entre as cargas são grandezas inversamente proporcionais ao quadrado da distância.
Construindo uma tabela que demonstra a relação entre a força
F e a distância d, tem-se:
|
Distância |
d/3 |
d/2 |
d |
2d |
3d |
4d |
|
Força |
|
|
F |
F/4 |
F/9 |
F/16 |
Então o gráfico F = f(d) será:
Constante Eletrostática
A constante de
proporcionalidade k depende do meio
onde os corpos se encontram e do sistema de unidades escolhido. No vácuo e
aproximadamente no ar, ela vale:
k = 9 . 109 N . m2
/ C2
Permissividade Absoluta
Quando as cargas são colocadas
num meio diferente do vácuo, a força elétrica sofre uma redução, dependendo do
meio. O fator de redução da força elétrica é denominada permissividade absoluta
do meio e representa-se por e. A tabela a seguir mostra
alguns valores de e.
|
Meio |
e |
|
Vácuo |
1,000 |
|
Ar |
1,005 |
|
Benzeno |
2,3 |
|
Âmbar |
2,7 |
|
Vidro |
4,5 |
|
Óleo |
4,6 |
|
Mica |
5,4 |
|
Glicerina |
43,0 |
|
Água |
81,0 |
Pode-se relacionar a
permissividade com a constante k, através da expressão:
Força eletrostática resultante